Competitive Signals and Systems MCQs – Signals and Systems Basics MCQs ( Signals and Systems ) MCQs
Latest Signals and Systems MCQs
By practicing these MCQs of Signals and Systems Basics MCQs ( Signals and Systems ) MCQs – Latest Competitive MCQs , an individual for exams performs better than before. This post comprising of objective questions and answers related to “ Signals and Systems Basics MCQs ( Signals and Systems ) Mcqs “. As wise people believe “Perfect Practice make a Man Perfect”. It is therefore practice these mcqs of Signals and Systems to approach the success. Tab this page to check ” Signals and Systems Basics MCQs ( Signals and Systems )” for the preparation of competitive mcqs, FPSC mcqs, PPSC mcqs, SPSC mcqs, KPPSC mcqs, AJKPSC mcqs, BPSC mcqs, NTS mcqs, PTS mcqs, OTS mcqs, Atomic Energy mcqs, Pak Army mcqs, Pak Navy mcqs, CTS mcqs, ETEA mcqs and others.
Signals and Systems MCQs – Signals and Systems Basics MCQs ( Signals and Systems ) MCQs
The most occurred mcqs of Signals and Systems Basics MCQs ( Signals and Systems ) in past papers. Past papers of Signals and Systems Basics MCQs ( Signals and Systems ) Mcqs. Past papers of Signals and Systems Basics MCQs ( Signals and Systems ) Mcqs . Mcqs are the necessary part of any competitive / job related exams. The Mcqs having specific numbers in any written test. It is therefore everyone have to learn / remember the related Signals and Systems Basics MCQs ( Signals and Systems ) Mcqs. The Important series of Signals and Systems Basics MCQs ( Signals and Systems ) Mcqs are given below:
System Classification and Properties – 1
1. The type of systems which are characterized by input and the output quantized at certain levels are called as
a) analog
b) discrete
c) continuous
d) digital
Answer: b
Explanation: Discrete systems have their input and output values restricted to enter some quantised/discretized levels.
2. The type of systems which are characterized by input and the output capable of taking any value in a particular set of values are called as
a) analog
b) discrete
c) digital
d) continuous
Answer: d
Explanation: Continuous systems have a restriction on the basis of the upper bound and lower bound, but within this set, the input and output can assume any value. Thus, there are infinite values attainable in this system
3. An example of a discrete set of information/system is
a) the trajectory of the Sun
b) data on a CD
c) universe time scale
d) movement of water through a pipe
Answer: b
Explanation: The rest of the parameters are continuous in nature. Data is stored in the form of discretized bits on CDs.
4. A system which is linear is said to obey the rules of
a) scaling
b) additivity
c) both scaling and additivity
d) homogeneity
Answer: c
Explanation: A system is said to be additive and scalable in order to be classified as a linear system.
5. A time invariant system is a system whose output
a) increases with a delay in input
b) decreases with a delay in input
c) remains same with a delay in input
d) vanishes with a delay in input
Answer: c
Explanation: A time invariant system’s output should be directly related to the time of the output. There should be no scaling, i.e. y(t) = f(x(t)).
6. Should real time instruments like oscilloscopes be time invariant?
a) Yes
b) Sometimes
c) Never
d) They have no relation with time variance
Answer: a
Explanation: Oscilloscopes should be time invariant, i.e they should work the same way everyday, and the output should not change with the time at which it is operated.
7. All real time systems concerned with the concept of causality are
a) non causal
b) causal
c) neither causal nor non causal
d) memoryless
Answer: b
Explanation: All real time systems are causal, since they cannot have perception of the future, and only depend on their memory.
8. A system is said to be defined as non causal, when
a) the output at the present depends on the input at an earlier time
b) the output at the present does not depend on the factor of time at all
c) the output at the present depends on the input at the current time
d) the output at the present depends on the input at a time instant in the future
Answer: d
Explanation: A non causal system’s output is said to depend on the input at a time in the future.
9. When we take up design of systems, ideally how do we define the stability of a system?
a) A system is stable, if a bounded input gives a bounded output, for some values of the input
b) A system is unstable, if a bounded input gives a bounded output, for all values of the input
c) A system is stable, if a bounded input gives a bounded output, for all values of the input
d) A system is unstable, if a bounded input gives a bounded output, for some values of the input
Answer: c
Explanation: For designing a system, it should be kept in mind that the system does not blow out for a finite input. Thus, every finite input should give a finite output.
10. All causal systems must have the component of
a) memory
b) time invariance
c) stability
d) linearity
Answer: a
Explanation: Causal systems depend on the functional value at an earlier time, compelling the system to possess memory.
System Classification and Properties – 2
1. Amplifiers, motors, filters etc. are examples for which type of system?
a) Distributed parameter systems
b) Unstable systems
c) Discrete time systems
d) Continuous time systems
Answer: d
Explanation: Amplifiers, motors, filters etc. are examples of continuous time systems as these systems operate on a continuous time input signal and produce a continuous time output signal. Whereas discrete time systems operate on discrete time signals, distributed parameter systems have signals which are functions of space as well as time and unstable systems produce unbounded output from bounded or unbounded input.
2. Which among the following systems are described by partial differential functions?
a) Causal Systems and Dynamic systems
b) Distributed parameter systems and linear systems
c) Distributed parameter systems and Dynamic systems
d) Causal systems and linear systems
Answer: c
Explanation: In distributed parameter systems, signals are functions of space as well as time. In dynamic systems the output depends on past, present and future values of input, hence, both of these systems are described by differential functions.
3. Which one of the following systems is causal?
a) y(t)=x(t)+x(t-3)+x(t2)
b) y(n)=x(n+2)
c) y(t)=x(t-1)+x(t-2)
d) y(n)=x(2n2)
Answer: c
Explanation: A causal system is one in which the output depends on the present or past values of the input, not future. If it depends on future values then it is non-causal. For y(t)=x(t)+x(t-3)+x(t2), y(n)=x(n+2), and y(n)=x(2n2), the output depends on future values i.e., x (t2), x (n + 2) and x (2n2) respectively. Whereas in y(t)=x(t-1)+x(t-2), the output y(t) depends on past values only i.e., x(t – 1) and x(t – 2).
4. Which among the following is not a linear system?
Answer: a
Explanation: Here is the Explanation.
5. 
a) Static, linear, causal and time variant
b) Dynamic, non – linear, causal and time invariant
c) Static, non – linear, causal and time variant
d) Dynamic, non – linear, causal and time variant
Answer: b
Explanation: Here is the Explanation.
6. Which one of the following is an example of a bounded signal?
a) et coswt
b) et sinw(-t)
c) e-t coswt
d) et cosw(-t)
Answer: c
Explanation: A bounded signal is the one which satisfies the condition |x(t)|< M < ∞ for all t.
Clearly, the signals et coswt, et sinw(-t) and et cosw(-t) are exponentially growing signals as the power of the function is positive i.e., the signals will grow beyond infinity. Whereas the signal e-t coswt is an exponentially decaying signal, hence it will decay to zero and will always be less than infinity. Therefore, it is bounded.
7. A system produces zero output for one input and same gives the same output for several other inputs. What is the system called?
a) Non – invertible System
b) Invertible system
c) Non – causal system
d) Causal system
Answer: a
Explanation: A system is said to be invertible if the input fed to the system can be retrieved from the output of the system. Otherwise the system is non-invertible. Also, if a system gives zero output for any input and gives the same output for many inputs, then the system is non-invertible.
8. Which among the following is a LTI system?
a) dy(t)/dt+ty(t)=x(t)
b) y(t)=x(t)cosπt
c) y(n)=x(n)+nx(n-1)
d) y(n)=x3 (n+1)
Answer: d
Explanation: A system is said to be linear time invariant (LTI) if the input-output characteristics do not change with time.
This expression has a coefficient which is a function of time. ∴ the system is time variant.
Output when input is delayed by T, y(t,T)=x(t-T)cosπt
If the output is delayed by T, y(t-T)=x(t-T)cosπ(t-T)
Clearly, both expressions are not equal ∴ The system is time variant.
Output when input is delayed by N, y(n,N)=x(n-N)+nx(n-1-N)
If the output is delayed by N, y(n-N)=x(n-N)+(n-N)x(n-1-N)
Clearly, both expressions are not equal ∴ The system is time variant.
Output when input is delayed by N, y(n,N)=x3 (n+1-N)
If the output is delayed by N, y(n-N)= x3 (n+1-N)
Clearly, both expressions are equal. ∴ The system is time invariant.
Signal Classification and Properties – 1
1. Which of the following signals are monotonic in nature?
a) 1-exp(-t)
b) 1-exp(sin(t))
c) log(tan(t))
d) cos(t)
Answer: a
Explanation: All of the other functions have a periodic element in them, which means the function attains the same value after a period of time, which should not occur for a monotonic function.
2. What is the period of the following signal, x(t) = sin(18*pi*t + 78 deg)?
a) 1⁄9
b) 2⁄9
c) 1⁄3
d) 4⁄9
Answer: b
Explanation: The signal can be expressed as sin(wt + d), where the time period = 2*pi/w.
3. Which of the following signals is monotonic?
a) x(t) = t3 – 2t
b) x(t) = sin(t)
c) x(t) = sin22(t) + cos22(t) – 2t
d) x(t) = log(cos(t))
Answer: c
Explanation: c) reduces to 1 – 2t, which is a strictly decreasing function.
4. For the signal, x(t) = log(cos(a*pi*t+d)) for a = 50 Hz, what is the time period of the signal, if periodic?
a) 0.16s
b) 0.08s
c) 0.12s
d) 0.04s
Answer: d
Explanation: Time period = 2*pi/(50)pi = 1/25 = 0.04s
5. What are the steady state values of the signals, 1-exp(-t), and 1-k*exp(-k*t)?
a) 1, k
b) 1, 1/k
c) k, k
d) 1, 1
Answer: d
Explanation: Consider limit at t tending to infinity, we obtain 1 for both cases.
6. For a bounded function, is the integral of the function from -infinity to +infinity defined and finite?
a) Yes
b) Never
c) Not always
d) None of the mentioned
Answer: c
Explanation: If the bounded function, is say y = 2, then the integral ceases to hold. Similarly, if it is just the block square function, it is finite. Hence, it depends upon the spread of the signal on either side. If the spread is finite, the integral will be finite.
7. For the signal x(t) = a – b*exp(-ct), what is the steady state value, and the initial value?
a) c, b
b) c, c-a
c) a, a-b
d) b, a-b
Answer: c
Explanation: Put the limits as t tends to infinity and as t tends to zero.
8. For a double sided function, which is odd, what will be the integral of the function from -infinity to +infinity equal to?
a) Non-zero Finite
b) Zero
c) Infinite
d) None of the mentioned
Answer: b
Explanation: For an odd function, f(-x) = -f(x), thus the integrals will cancel each other, giving zero.
9. Find where the signal x(t) = 1/(t2 – 3t + 2) finds its maximum value between (1.25, 1.75):
a) 1.40
b) 1.45
c) 1.55
d) 1.50
Answer: d
Explanation: Differentiate the function for an optima, put it to zero, we will obtain t = 1.5 as the required instant.
10. Is the signal x(t) = exp(-t)*sin(t) periodic in nature?
a) Yes
b) No
Answer: b
Explanation: Though sin(t) is a periodic function, exp(-t) is not a periodic function, thus leading to non-periodicity.
Signal Classification and Properties – 2
1. A signal is a physical quantity which does not vary with ____________
a) Time
b) Space
c) Independent Variables
d) Dependent Variables
Answer: d
Explanation: A signal is a physical quantity which varies with time, space or any other independent variables. Therefore, it does not vary with dependent variables.
2. Most of the signals found in nature are _________
a) Continuous-time and discrete-time
b) Continuous-time and digital
c) Digital and Analog
d) Analog and Continuous-time
Answer: d
Explanation: Signals naturally are continuous-time signals. These are also known as analog signals. Continuous-time or analog signals are defined for all values of time t.
3. Which one of the following is not a characteristic of a deterministic signal?
a) Exhibits no uncertainty
b) Instantaneous value can be accurately predicted
c) Exhibits uncertainty
d) Can be represented by a mathematical equation
Answer: c
Explanation: Deterministic signal is one which exhibits no uncertainty and its instantaneous value can be accurately predicted from its mathematical equation. Therefore, a deterministic signal doesn’t exhibit uncertainty. However, a random is always uncertain.
4. Determine the fundamental period of the following signal:sin60t.
a) 1/60 sec
b) 1/30 sec
c) 1/20 sec
d) 1/10 sec
Answer: b
Explanation: Consider the equation: sinΩ0t. Comparing this equation with the one given in the question: sin60t
⇒ Ω0=60π
5. Sum of two periodic signals is a periodic signal when the ratio of their time periods is ____________
a) A rational number
b) An irrational number
c) A complex number
d) An integer
Answer: a
Explanation: Sum of two periodic signals is a periodic signal only when the ratio of their time periods is a rational number or it is the ratio of two integers. For e.g., T1/T2 = 5/7 → Periodic; T1/T2 = 5 → Aperiodic.
6. Determine the Time period of: x(t)=3 cos(20t+5)+sin(8t-3).
a) 1/10 sec
b) 1/20 sec
c) 2/5 sec
d 2/4 sec
Answer: c
Explanation: Here is the explanation.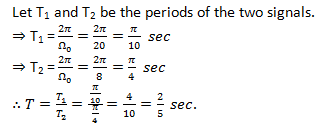
7. What is the even component of a discrete-time signal?
Answer: b
Explanation: Here is the explanation.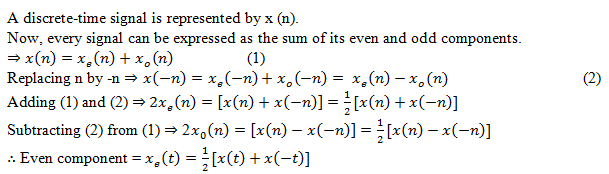
8. Determine the odd component of the signal: x(t)=cost+sint.
a) sint
b) 2sint
c) cost
d) 2cost
Answer: c
Explanation: Here is the explanation.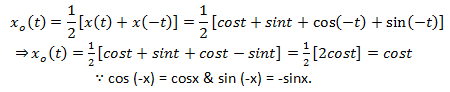
9. Is the signal sin(t) anti-symmetric?
a) YES
b) NO
Answer: a
Explanation: A signal is said to be anti-symmetric or odd signal when it satisfies the following condition:
⇒ x(t) = – x(t)
Now, here, x(t) = sin(t) ⇒ x(-t) = sin(-t) = – sin(t)
∴ Sin(t) is an anti-symmetric signal or an odd signal.
10. For an energy signal __________
a) E=0
b) P= ∞
c) E= ∞
d) P=0
Answer: d
Explanation: A signal is called an energy signal if the energy satisfies 0<E< ∞ and power P=0.
11. Determine the power of the signal: x(t) = cos(t).
a) 1/2
b) 1
c) 3/2
d) 2
Answer: a
Explanation: Here is the explanation.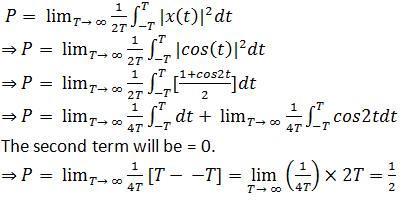
12. Is the following signal an energy signal?
x(t) = u(t) – u(t – 1)
a) YES
b) NO
Answer: a
Explanation: Here is the explanation.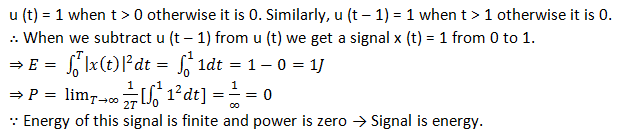
13. A signal is anti-causal if ______________
a) x(t) = 0 for t = 0
b) x(t) = 1 for t < 0
c) x(t) = 1 for t > 0
d) x(t) = 0 for t > 0
Answer: d
Explanation: A signal is said to be anti-causal when x(t) = 0 for t > 0.
14. Is the signal x(t)= eat u(t) causal?
a) YES
b) NO
Answer: a
Explanation: A signal is said to be causal if it is 0 for t < 0.
Now, we know, u(t) = 1 for t ≥ 0.
∴ x(t)= eat for t ≥0 .
∴ The signal is 0 for t < 0.
∴ The signal is causal.
15. Is the signal x(n) = u(n + 4) – u(n – 4) causal?
a) YES
b) NO
Answer: b
Explanation: A signal is said to be causal if it is 0 for t < 0.
⇒ u (n + 4) = 1 for n ≥ – 4
⇒ u(n – 4) = 1 for n ≥ 4
∴ The signal x (t) is defined for the interval [-4, 4] and it is zero for all other n values.
∵ The signal is defined for both n > 0 and n < 0
∴ The signal is non-causal.
Classification of Signals
1. What is single-valued function?
a) Single value for all instants of time
b) Unique value for every instant of time
c) A single pattern is followed by after ‘t’ intervals
d) Different pattern of values is followed by after ‘t’ intervals of time
Answer: b
Explanation: Single-valued function means “for every instant of time there exists unique value of the function”.
2. In real valued function and complex valued function, time is _______________
a) Real
b) Complex
c) Imaginary
d) Not predictable
Answer: a
Explanation: Time is an independent variable and it is real valued irrespective of real valued or complex valued function. And time is always real.
3. Discrete time signal is derived from continuous time signal by _____________ process.
a) Addition
b) Multiplying
c) Sampling
d) Addition and multiplication
Answer: c
Explanation: Sampling is a process wherein continuous time signal is converted to its equivalent discrete time signal. It is given by t = N*t.
4. Even signals are symmetric about the vertical axis.
a) True
b) False
Answer: a
Explanation: Signals are classified as even if it has symmetry about its vertical axis. It is given by the equation x (-t) = x (t).
5. If x (-t) = -x (t) then the signal is said to be _____________
a) Even signal
b) Odd signal
c) Periodic signal
d) Non periodic signal
Answer: a
Explanation: Signals is said to be odd if it is anti- symmetry over the time origin. And it is given by the equation x (-t) = -x (t).
6. Which of the following is true for complex-valued function?
a) X (-t) = x*(t)
b) X (-t) = x(t)
c) X (-t) = – x(t)
d) X (-t) = x*(-t)
Answer: a
Explanation: Complex-valued function is said to be conjugate symmetry if its real part is even and imaginary part is odd and it is shown by the equation x(-t) = x*(t).
7. When x(t ) is said to be non periodic signal?
a) If the equation x (t) = x (t + T) is satisfied for all values of T
b) If the equation x (t) = x (t + T) is satisfied for only one value of T
c) If the equation x (t) = x (t + T) is satisfied for no values of T
d) If the equation x (t) = x (t + T) is satisfied for only odd values of T
Answer: c
Explanation: A signal x (t) is said to be non periodic signal if it does not satisfy the equation x(t) = x(t + T). And it is periodic if it satisfies the equation for all values of T = T0, 2T0, 3T0…
8. Fundamental frequency x[n] is given by ___________
a) Omega = 2*pi /N
b) Omega = 2*pi*N
c) Omega = 4*pi *2N
d) Omega = pi / N
Answer: a
Explanation: Fundamental frequency is the smallest value of N which satisfies the equation
Omega = 2*pi/ N, Where N is a positive integer.
9. Noise generated by an amplifier of radio is an example for?
a) Discrete signal
b) Deterministic signal
c) Random signal
d) Periodic signal
Answer: c
Explanation: Random signal is the one which there is uncertainty before its actual occurrence. Noise is a best example for random signal.
10. Energy signal has zero average power and power signal has zero energy.
a) True
b) False
Answer: b
Explanation: Energy and power signals are mutually exclusive. Energy signal has zero average power and power signal has infinite energy.
11. What is the fundamental frequency of discrete –time wave shown in fig a?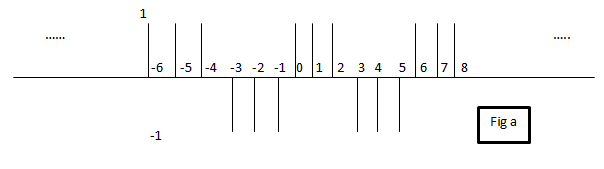
a) π/6
b) π/3
c) 2π/8
d) π
Answer: b
Explanation: Omega = 2* π / N. In the given example the number of samples in one period is N = 6. By substituting the value of N =6 in the above equation then we get fundamental frequency as π/3.
12. Calculate the average power of the discrete-time wave shown in fig a?
a) 1
b) 6
c) 0
d) -1
Answer: a
Explanation: The given formula is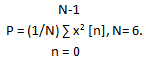 
used to calculate average power for Periodic -discrete signal. By substituting the value of N and x2[n] in the given then we get the required answer.
13. What is the total energy of rectangular pulse shown in fig b?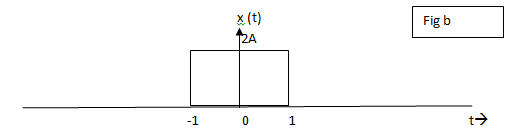
a) 8A2
b) 4A
c) 2A
d) 4A2
Answer: a
Explanation: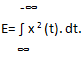 
The total energy of the rectangular pulse can be found by integrating the square of the signal. Basically energy is given by area under the curve.
14. What is the total power of the rectangular pulse shown in fig b?
a) 0
b) 8A2
c) ∞
d) 2A
Answer: a
Explanation: Energy signals have zero power and finite energy. Figure b is an example of an energy signal. This is one of the definition/ properties of the energy signal.
15. What is the total energy of the signal shown in fig c?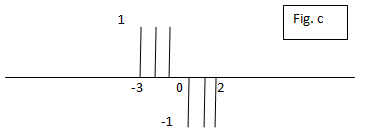
a) 6
b) 0
c) 3
d) 1
Answer: a
Explanation: The given figure is an example of an energy signal hence the energy of a discrete-time signal is given by the equation E = ∑ x2[n].
Basic Operations on Signals – 1
1. Which of the following is an example of amplitude scaling?
a) Electronic amplifier
b) Electronic attenuator
c) Both amplifier and attenuator
d) Adder
Answer: c
Explanation: Amplitude scaling refers to multiplication of a constant with the given signal.
It is given by y (t) = a x (t). It can be both increase in amplitude or decrease in amplitude.
2. Resistor performs amplitude scaling when x (t) is voltage, a is resistance and y (t) is output current.
a) True
b) False
Answer: b
Explanation: The given statement is not true. The relation between voltage, current and resistance is given by V = IR. Comparing with equation y (t) = a x (t), we can see that y (t) is the output voltage for given current x (t) with resistance R.
3. Which of the following is an example of physical device which adds the signals?
a) Radio
b) Audio mixer
c) Frequency divider
d) Subtractor
Answer: b
Explanation: Audio mixer is a device which combines music and voice signals. It is given by
Y (t) = x1 (t) + x2 (t).
4. AM radio signal is an example for __________
a) y (t) = a x (t)
b) y (t) = x1 (t) + x2 (t)
c) y (t) = x1 (t) * x2 (t)
d) y (t) = -x(t)
Answer: c
Explanation: AM radio signal is an example for y (t) = x1 (t) * x2 (t) where, x1 (t) consists of an audio signal plus a dc component and x2 (t) is a sinusoidal signal called carrier wave.
5. Which of the passive component performs differentiation operation?
a) Resistor
b) Capacitor
c) Inductor
d) Amplifier
Answer: c
Explanation: Inductor performs differentiation. It is given by y (t) = L d/dt i(t) where, I (t) denotes current flowing through an inductor of inductance L.
6. Which of the component performs integration operation?
a) Resistor
d) Diode
c) Capacitor
d) Inductor
Answer: c
Explanation: Capacitor performs integration. V (t) developed across capacitor is given by
v (t) = (1/C)* ∫t-∞ i (∂).d∂, I (t) is the current flowing through a capacitor of capacitance C.
7. Time scaling is an operation performed on _______
a) Dependent variable
b) Independent variable
c) Both dependent and independent variable
d) Neither dependent nor independent variable
Answer: b
Explanation: Time scaling is an example for operations performed on independent variable time.
It is given by y (t) = x (at).
8. Y (t) = x (2t) is ________
a) Compressed signal
b) Expanded signal
c) Shifted signal
d) Amplitude scaled signal by a factor of 2
Answer: a
Explanation: By comparing the given equation with y (t) = x (at) we get a=2. If a>1 then it is compressed version of x (t).
9. Y (t) = x (t/5) is _______
a) Compressed signal
b) Expanded signal
c) Time shifted signal
d) Amplitude scaled signal by factor 1/5
Answer: b
Explanation: y (t) = x (at), comparing this with the given expression we get a = 1/5. If 0<a<1 then it is expanded (stretched) version of x (t).
10. In discrete signal, if y [n] = x [k*n] and k>1 then ______
a) Some samples are lost from x [n]
b) Some samples are added to x [n]
c) It has no effect on samples
d) Samples will be increased with factor k
Answer: a
Explanation: For discrete time signal y [n] = x [k*n] and k>1, it will be compressed signal and some samples will be lost. The samples lost will not violate the rules of sampling theorem.
Basic Operations on Signals – 2
1. Considering Figure 1, sketch y= 2* x (t).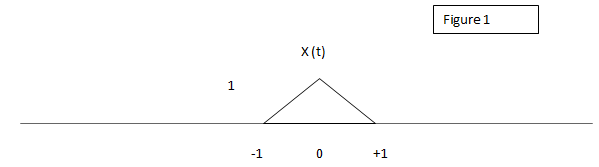
Answer: a
Explanation: Y (t) = 2*x (t) is an example for amplitude scaling. Here amplitude is scaled by a factor 2.
2. Considering Figure 1, sketch y= -3* x (t).
a)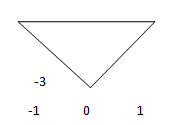
b)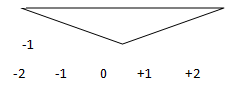
c)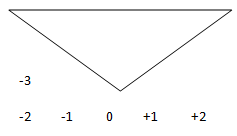
d)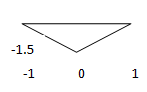
Answer: a
Explanation: Y (t) = -3*x (t) is an example for amplitude scaling. Here amplitude is scaled by a factor -3.
3. In the following diagram, X [n] and y [n] are related by ______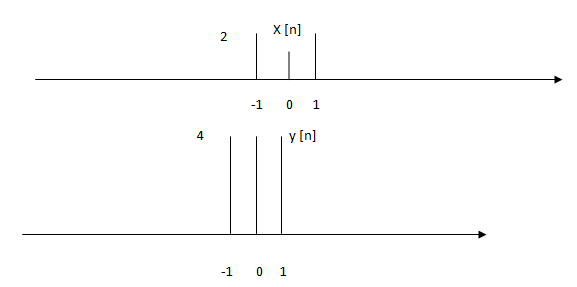
a) Y [n] = 2*x [n]
b) Y [n] = -2*x [n]
c) Y [n] = x [2n]
d) Y [n] = x [-2n]
Answer: a
Explanation: Y [n] = 2*x [n] is an example for amplitude scaling of discrete time signal. The given figure is an example for 2*x [n] hence Y [n] = 2*x [n] is correct.
4. X [n] and y [n] is as shown below, the relationship between x [n] and y [n] is given by ______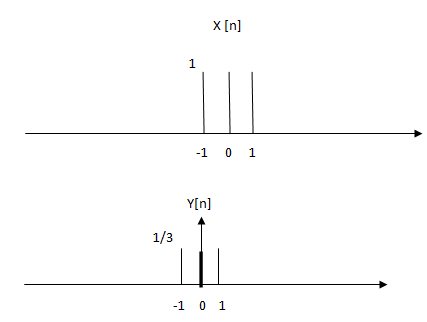
a) X [n] = y [n]/3
b) X [n] = 3* y [n]
c) Y [n] = x [n]/3
d) Y [n] = 3*x [n]
Answer: c
Explanation: The given y [n] is amplitude scaling of a discrete time signal by a factor 1/3.
Hence the amplitude is reduced by 1/3.
5. Considering figure 3 above, is the following figure true for y [n] = x [2n]?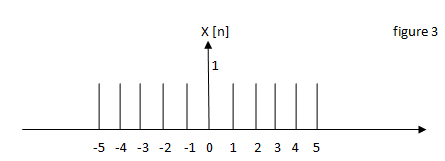
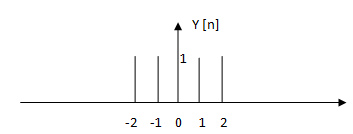
a) True
b) False
Answer: a
Explanation: X [2n] is an example of time scaling. For discrete time signal x [k*n], k>1 the samples will be lost.
6. Considering figure 3 above, is the following figure true for y [n] = x [n/2]?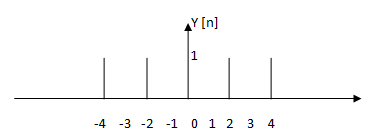
a) True
b) False
Answer: b
Explanation: X [n/2] is an example for time scaling by factor ½ and it will be a stretched signal. The discrete time signal should extend from -10 to 10.
7. Consider figure 4, is the given y (t) an integration of x (t)?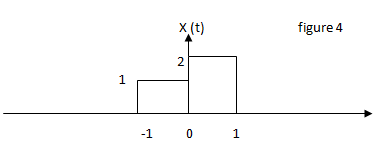
a) Y (t) = ∫x (t).dt
b) Y (t) = ∫x2 (t).dt
c) Y (t) = 3* ∫x (t).dt
d) Y (t) = 3* ∫x2 (t).dt
Answer: a
Explanation: The given y (t) is integral of x (t) and amplitude 3 remains constant for t>1.
It is because of the properties of integration.
8. . Consider figure 4, is the given y (t) a differentiation of x (t)?
Answer: a
Explanation: The given y (t) is differentiation of x (t) and hence we have impulses at -1, 0 and 1.
9. The given pair x (t) and y (t) is _______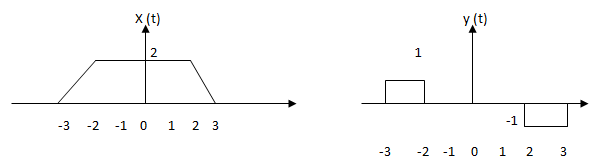
a) Y (t) = d/dt (x (t))
b) Y (t) = ∫x (t).dt
c) Y (t) = x (t) -1
d) Y (t) = x (t) /2
Answer: a
Explanation: The given pair x (t) and y (t) is related by y (t) = d/dt (x (t)). From -2 to 2 we have Y (t) is zero because differentiation of constant is zero.
10. The given pair x (t) and y (t) is related by _______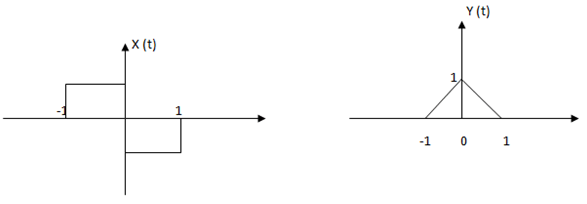
a) Y (t) = d/dt (x (t))
b) Y (t) = x (t) + 1
c) Y (t) = ∫x (t) .dt
d) Not related
Answer: c
Explanation: The given pair x (t) and y (t) is related by Y (t) = ∫x (t) .dt. The integral of x (t) gives the Y (t). Y (t) = 0 for t > 1.
Elementary Signals – 1
1. The general form of real exponential signal is________
a) X (t) = beat
b) X (t) = (b+1)eat
c) X (t) = b (at)
d) X (t) = be (a+1)t
Answer: a
Explanation: X (t) = beat is the most general way of representing the exponential signals where both b and a are real parameters.
2. In the equation x (t) = beat if a < 0, then it is called ______
a) Growing exponential
b) Decaying exponential
c) Complex exponential
d) Both Growing and Decaying exponential
Answer: b
Explanation: If a > 0 in x (t) = beat it is called growing exponential and if <0 it is called decaying exponential. Hence Decaying exponential is correct.
3. In the below figure if R value is increased then which of the following is true?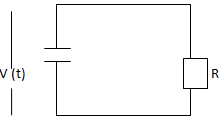
a) Slower the rate of decay of v (t)
b) Greater the rate of decay of v (t)
c) Decay rate is independent of R
d) Decay rate depends only on the capacitor value
Answer: a
Explanation: In the circuit shown voltage across capacitor decays exponentially with time at a rate determined by time constant RC. Hence the larger the resistor, the slower will be the rate of decay of v (t) with time.
4. The time period of continuous-time sinusoidal signal is given by _____
a) T = 2π / w
b) T = 2π / 3w
c) T = π / w
d) T = π / 2w
Answer: a
Explanation: X (t) = A cos (wt+φ) is the continuous-time sinusoidal signal and its period is given by
T = 2π / w where w is the frequency in radians per second.
5. The natural angular frequency of the parallel LC circuit is?
Answer: a
Explanation: Wo is the natural angular frequency and for parallel LC circuit it is given by wo=1⁄√LC where, L is value of inductor and C is value of capacitor.
6. X [n] = 2 cos (2n) is periodic or not?
a) Periodic with period 2n
b) Periodic with period 2π
c) Periodic with period 2
d) Non periodic
Answer: d
Explanation: The given signal x [n] is non periodic as it doesn’t satisfy the equation w=2πm⁄N where, N is fundamental period and m is an integer.
7. Check whether x [n] = 7 sin (6πn) is periodic and if it is period calculate its fundamental period?
a) Periodic with fundamental period 6π
b) Periodic with fundamental period 3
c) Periodic with fundamental period 1
d) Non periodic
Answer: c
Explanation: X [n] = 7 sin (6πn) is a periodic discrete time signal with period 1. By substituting w = 6π and m=3 in w=2πm⁄N we get N =1.
8. Find the smallest angular frequency for which the discrete time signal with fundamental period N=8 would be periodic?
a) π⁄4
b) π⁄2
c) 3π⁄4
d) π⁄16
Answer: a
Explanation: By substituting N=8 and m=1 in the equation w=2πm⁄N we get the smallest angular frequency as π⁄4.
9. Euler’s identity ejθ is expanded as _____
a) cos θ + j sin θ
b) cos θ – j sin θ
c) cos θ + j sin 2θ
d) cos 2θ+j sinθ
Answer: a
Explanation: The complex exponential ejθ is expanded as cos θ + j sin θ and is called Euler’s identity with cos θ as real part sin θ as imaginary part.
10. Exponentially damped sinusoidal signal is ______
a) Periodic
b) Non periodic
c) Insufficient information
d) Maybe periodic
Answer: b
Explanation: Exponentially damped sinusoidal signal of any kind is not periodic as it does not satisfy the periodicity condition.
Elementary Signals – 2
1. Mathematical representation of given rectangular pulse is ______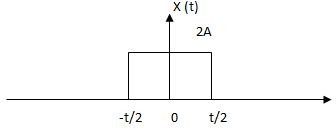
a) X (t) = {2A, t/2 < 0 < -t/2
b) X (t) = {2A, -t/2 < 0 < t/2
c) X (t) = {2A, 0 <= |t| <= t/2
{0, |t| > t/2
d) X (t) = {2A, 0 <|t| < t/2
{0, |t| > t/2
Answer: c
Explanation: The given rectangular pulse is of amplitude 2A for the time interval –t/2 to t/2 and zero otherwise.
2. If 
describe x [n] as superposition of two step functions.
a) X [n] = u [n] – u [n-5].
b) X [n] = u [n] + u [n-5].
c) X [n] = u [n-5] – u [n].
d) X [n] = u [n-5] + u [n].
Answer: a
Explanation: X [n] will be of amplitude for the interval 0 to 4 and zero otherwise. It can be obtained by the equation x [n] = u [n] – u [n-5].
3. Discrete-time version of unit impulse is defined as ______
Answer: a
Explanation: Unit impulse is an elementary signal with zero amplitude everywhere except at n = 0.
4. Which of the following is not true about unit impulse function?
Answer: d
Explanation: One option gives the definition of discrete-time version of impulse function, other options gives continuous-time representation of impulse function.
5. The step function u (t) is integral of _______ with respect to time t.
a) Ramp function
b) Impulse function
c) Sinusoidal function
d) Exponential function
Answer: b
Explanation: Step function is an integral of impulse function and conversely, impulse is the derivative of step function u (t).
6. The area under the pulse defines _____ of the impulse.
a) Strength
b) Energy
c) Power
d) Duration
Answer: a
Explanation: The area under the pulse defines strength of the impulse and the strength of the impulse is denoted by the label next to the arrow.
7. Unit impulse ∂(t) is _____ of time t.
a) Odd function
b) Even function
c) Neither even nor odd function
d) Odd function of even amplitude
Answer: b
Explanation: For an impulse function, ∂(-t)= ∂(t). Hence unit impulse is an even function of time t.
8. Shifting property of impulse ∂(t) is given by ______
Answer: a
Explanation: X (t) be a function and the product of x (t) with time shifted delta function ∂(t – to) gives x(to), this is referred to as shifting property of impulse function.
9. ∂(at) = 1⁄a ∂(t), this property of unit impulse is called ______
a) Time shifting property
b) Time scaling property
c) Amplitude scaling property
d) Time reversal property
Answer: b
Explanation: Impulse function exhibits shifting property, time scaling property. And time scaling property is given by∂(at) = 1⁄a ∂(t).
10. Which of the following is not true about the ramp function?
a) 
b) r (t) = t u (t)
c) Ramp function with unit slope is integral of unit step
d) Integral of unit step is a ramp function of unit slope
Answer: d
Explanation: The impulse function is derivative of the step function. In the same way the integral of step function is a ramp function of unit slope.
∫u(t) = r(t).