Digital Signal Processing MCQs – Multirate Digital Signal Processing MCQs ( Digital Signal Processing ) MCQs

Latest Digital Signal Processing MCQs
By practicing these MCQs of Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) MCQs – Latest Competitive MCQs , an individual for exams performs better than before. This post comprising of objective questions and answers related to “Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) Mcqs “. As wise people believe “Perfect Practice make a Man Perfect”. It is therefore practice these mcqs of Digital Signal Processing to approach the success. Tab this page to check “Multirate Digital Signal Procesing MCQs ( Digital Signal Processing )” for the preparation of competitive mcqs, FPSC mcqs, PPSC mcqs, SPSC mcqs, KPPSC mcqs, AJKPSC mcqs, BPSC mcqs, NTS mcqs, PTS mcqs, OTS mcqs, Atomic Energy mcqs, Pak Army mcqs, Pak Navy mcqs, CTS mcqs, ETEA mcqs and others.
Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) MCQs – Digital Signal Processing MCQs
The most occurred mcqs of Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) in past papers. Past papers of Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) Mcqs. Past papers of Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) Mcqs . Mcqs are the necessary part of any competitive / job related exams. The Mcqs having specific numbers in any written test. It is therefore everyone have to learn / remember the related Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) Mcqs. The Important series of Multirate Digital Signal Procesing MCQs ( Digital Signal Processing ) Mcqs are given below:
Multirate Digital Signal Processing
1. There is no requirement to process the various signals at different rates commensurate with the corresponding bandwidths of the signals.
a) True
b) False
Answer: b
Explanation: In telecommunication systems that transmit and receive different types of signals, there is a requirement to process the various signals at different rates commensurate with the corresponding bandwidths of the signals.
2. What is the process of converting a signal from a given rate to a different rate?
a) Sampling
b) Normalizing
c) Sampling rate conversion
d) None of the mentioned
Answer: c
Explanation: The process of converting a signal from a given rate to a different rate is known as sampling rate conversion.
3. The systems that employ multiple sampling rates are called multi-rate DSP systems.
a) True
b) False
Answer: a
Explanation: Systems that employ multiple sampling rates in the processing of digital signals are called multi rate digital signal processing systems.
4. Which of the following methods are used in sampling rate conversion of a digital signal?
a) D/A convertor and A/D convertor
b) Performing entirely in digital domain
c) None of the mentioned
d) D/A convertor, A/D convertor & Performing entirely in digital domain
Answer: d
Explanation: Sampling rate conversion of a digital signal can be accomplished in one of the two general methods. One method is to pass the signal through D/A converter, filter it if necessary, and then to resample the resulting analog signal at the desired rate. The second method is to perform the sampling rate conversion entirely in the digital domain.
5. Which of the following is the advantage of sampling rate conversion by converting the signal into analog signal?
a) Less signal distortion
b) Quantization effects
c) New sampling rate can be arbitrarily selected
d) None of the mentioned
Answer: c
Explanation: One apparent advantage of the given method is that the new sampling rate can be arbitrarily selected and need not have any special relationship with the old sampling rate.
6. Which of the following is the disadvantage of sampling rate conversion by converting the signal into analog signal?
a) Signal distortion
b) Quantization effects
c) New sampling rate can be arbitrarily selected
d) Signal distortion & Quantization effects
Answer: d
Explanation: The major disadvantage by the given type of conversion is the signal distortion introduced by the D/A converter in the signal reconstruction and by the quantization effects in the A/D conversion.
7. In which of the following, sampling rate conversion are used?
a) Narrow band filters
b) Digital filter banks
c) Quadrature mirror filters
d) All of the mentioned
Answer: d
Explanation: There are several applications of sampling rate conversion in multi rate digital signal processing systems, which include the implementation of narrow band filters, quadrature mirror filters and digital filter banks.
8. Which of the following use quadrature mirror filters?
a) Sub band coding
b) Trans-multiplexer
c) Sub band coding & Trans-multiplexer
d) None of the mentioned
Answer: c
Explanation: There are many applications where quadrature mirror filters can be used. Some of these applications are sub-band coding, trans-multiplexers and many other applications.
9. The sampling rate conversion can be as shown in the figure below.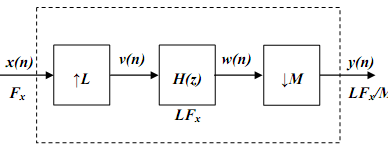
a) True
b) False
Answer: a
Explanation: The process of sampling rate conversion in the digital domain can be viewed as a linear filtering operation as illustrated in the given figure.
10. If Fx and Fy are the sampling rates of the input and output signals respectively, then what is the value of Fy/Fx?
a) D/I
b) I/D
c) I.D
d) None of the mentioned
Answer: b
Explanation: The input signal x(n) is characterized by the sampling rate Fx and he output signal y(m) is characterized by the sampling rate Fy, then
Fy/Fx = I/D
where I and D are relatively prime integers.
11. What is the process of reducing the sampling rate by a factor D?
a) Sampling rate conversion
b) Interpolation
c) Decimation
d) None of the mentioned
Answer: c
Explanation: The process of reducing the sampling rate by a factor D, i.e., down-sampling by D is called as decimation.
12. What is the process of increasing the sampling rate by a factor I?
a) Sampling rate conversion
b) Interpolation
c) Decimation
d) None of the mentioned
Answer: b
Explanation: The process of increasing the sampling rate by an integer factor I, i.e., up-sampling by I is called as interpolation.
Decimation by a Factor D
1. If we down-sample a signal x(n), then the resulting signal will be an aliased version of x(n).
a) True
b) False
Answer: a
Explanation: We know that if we reduce the sampling rate simply by selecting every Dth value of x(n), the signal will be an aliased version of x(n).
2. What is the folding frequency for the aliased version of x(n) with sampling rate F?
a) F/D
b) F/4D
c) F/2
d) F/2D
Answer: d
Explanation: We know that if we reduce the sampling rate simply by selecting every Dth value of x(n), the signal will be an aliased version of x(n), with a folding frequency of F/2D.
3. To what value should the bandwidth of x(n) has to be reduced in order to avoid aliasing?
a) F/D
b) F/2D
c) F/4D
d) None of the mentioned
Answer: b
Explanation: To avoid aliasing, we must reduce the bandwidth of x(n) to Fmax=F/2D. Then we may down-sample by D and thus avoid sampling.
4. Which process has a block diagram as shown in the figure below?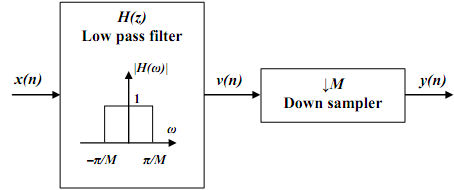
a) Sampling rate conversion
b) Interpolation
c) Decimation
d) None of the mentioned
Answer: c
Explanation: The block diagram shown in the figure is of sampling rate conversion by decimation by a factor D technique.
5. Which of the following is true about the filtering operation on x(n)?
a) Linear
b) Time variant
c) None of the mentioned
d) Linear and time invariant
Answer: d
Explanation: Although the filtering operation on x(n) is linear and time invariant, the down-sampling operation in combination with the filtering results in a time variant system.
6. If x(n) produces y(m), then x(n-n0) does imply y(n-n0) for any value of n0.
a) True
b) False
Answer: b
Explanation: Given the fact that x(n) produces y(m), we note that x(n-n0) does not imply y(n-n0) unless n0 is a multiple of D.
7. The linear filtering operation followed by down sampling on x(n) is not time invariant.
a) True
b) False
Answer: a
Explanation: Given the fact that x(n) produces y(m), we note that x(n-n0) does not imply y(n-n0) unless n0 is a multiple of D. Consequently, the overall linear operation, that is linear filtering followed by down sampling on x(n) is not time invariant.
8. Which of the following gives the equation for y(m)?
a) v(mD)
b) p(mD)
c) v(mD).p(mD)
d) none of the mentioned
Answer: c
Explanation: We know that the equation for y(m) is given as
y(m)= v¯(mD)= v(mD).p(mD).
9. We need not relate the spectrum of y(m) to spectrum of x(n) to obtain frequency response characteristic of y(m).
a) True
b) False
Answer: b
Explanation: The frequency domain characteristic of the output sequence y(m) can be obtained by relating the spectrum of y(m) to the spectrum of the input sequence x(n).
10. The sequence v¯(n) can be obtained by multiplying v(n) with a signal p(n) of period D.
a) True
b) False
Answer: a
Explanation: v¯(n) can be viewed as a sequence obtained by multiplying v(n) with a periodic train of impulses p(n) with period D.
11. If HD(ω) is the frequency response of the low pass filter, then for what value of ω, HD(ω)=1?
a) |ω| = π/D
b) |ω| ≥ π/D
c) |ω| ≤ π/D
d) None of the mentioned
Answer: c
Explanation: The input sequence x(n) is passed through a low pass filter, characterized by the impulse response h(n) and a frequency response HD(ω), which ideally satisfies the condition,
HD(ω)=1, |ω| ≤ π/D
=0, otherwise.
12. The filter eliminates the spectrum of X(ω) in the range π/D < ω < π.
a) True
b) False
Answer: a
Explanation: The input sequence x(n) is passed through a low pass filter, characterized by the impulse response h(n) and a frequency response HD(ω), which ideally satisfies the condition,
HD(ω)=1, |ω| ≤ π/D
=0, otherwise
Thus the filter eliminates the spectrum of X(ω) in the range π/D < ω < π.